Is it possible to stack matrices of different sizes. Math for dummies. Matrices and basic actions on them

Problems of linear algebra. The concept of a matrix. Types of matrices. Operations with matrices. Solving problems on the transformation of matrices.

When solving various problems of mathematics, one often has to deal with tables of numbers called matrices. With the help of matrices, it is convenient to solve systems of linear equations, perform many operations with vectors, solve various problems of computer graphics and other engineering tasks.

The matrix is ​​called a rectangular table of numbers containing a number m lines and some P columns. Numbers T And P are called matrix orders. If T = P, the matrix is ​​called square, and the number m = n- her order.

In the following, either double dashes or parentheses will be used to write matrices:

Or

For a short matrix designation, either a single large Latin letter (for example, A) or the symbol will often be used || a ij || and sometimes with an explanation: A = || a ij || = (aij), Where (i = 1, 2, ..., m, j=1, 2, ..., n).

Numbers aij , that are part of this matrix are called its elements. In recording aij first index і means the line number and the second index j- column number. In the case of a square matrix

(1.1)

the concepts of main and secondary diagonals are introduced. The main diagonal of the matrix (1.1) is the diagonal a 11 a 12 … ann going from the upper left corner of this matrix to its lower right corner. The side diagonal of the same matrix is ​​called the diagonal a n 1 a (n -1) 2… a 1 n , going from the lower left corner to the upper right corner.

Basic operations on matrices and their properties.

Let's move on to the definition of basic operations on matrices.

Matrix addition. The sum of two matrices A = || a ij || , Where And B = || b ij || , Where (i = 1, 2, ..., m, j=1, 2, ..., n) the same orders T And P is called the matrix C = || c ij || (i = 1,2, ..., m; j = 1, 2, ...., n) the same orders T And P, elements with ij which are determined by the formula

, Where (i = 1, 2, ..., m, j=1, 2, ..., n)(1.2)

To denote the sum of two matrices, we use the notation C \u003d A + B. The operation of composing the sum of matrices is called their addition. So, by definition:

+ =

From the definition of the sum of matrices, or rather from formulas (1.2), it directly follows that the operation of matrix addition has the same properties as the operation of addition of real numbers, namely:

1) commutative property: A + B = B + A,

2) combination property: ( A + B) + C = A + (B + C).

These properties make it possible not to care about the order of the terms of matrices when adding two or more matrices.

Multiplying a matrix by a number. The product of the matrix A = || a ij || , where (i = 1, 2, ..., m, j=1, 2, ..., n) by a real number l, is called the matrix C = || c ij || (i =1,2, ..., m; j = 1, 2, ...., n), the elements of which are determined by the formula:

, Where (i = 1, 2, ..., m, j=1, 2, ..., n)(1.3)

To denote the product of a matrix by a number, the notation is used C \u003d l A or C \u003d A l. The operation of compiling the product of a matrix by a number is called multiplying a matrix by this number.

It is clear from formula (1.3) that the multiplication of a matrix by a number has the following properties:

1) an associative property with respect to a numerical factor: (l m) A = l (m A);

2) distribution property with respect to the sum of matrices: l (A + B) = l A + l B;

3) distributive property with respect to the sum of numbers: (l + m) A = l A + m A

Comment. Difference of two matrices A And IN same orders T And P it is natural to call such a matrix WITH the same orders T And P, which in total with the matrix B gives the matrix A. The natural notation is used to denote the difference of two matrices: C \u003d A - B.

It is very easy to verify that the difference WITH two matrices A And IN can be obtained according to the rule C \u003d A + (-1) B.

Product of matrices or matrix multiplication.

Matrix product A = || a ij || , where (i = 1, 2, ..., m, j = 1, 2, ..., n) having orders, respectively, equal T And n, to matrix B = || b ij || , Where (i = 1, 2, ..., n , j=1, 2, ..., p), having orders, respectively, equal n And R, called matrix C = || c ij || (i = 1,2, ..., m; j = 1, 2, ...., p), which has orders, respectively, equal to T And R the elements of which are determined by the formula:

Where (i = 1, 2, ..., m, j = 1, 2, ..., p)(1.4)

To denote the product of a matrix A to matrix IN use record C = A × B. Matrix product operation A to matrix IN is called the multiplication of these matrices.

From the definition above, it follows that matrix A cannot be multiplied by any matrix B, it is necessary that the number of columns of the matrix A was equal to the number of matrix rows IN.

Formula (1.4) is a rule for compiling the elements of the matrix C, which is the product of the matrix A to matrix IN. This rule can also be formulated verbally: the element c i j standing at the intersection of the i-th row and the j-th column of the matrix C = A B is equal to the sum of the pairwise products of the corresponding elements of the i-th row of the matrix A and the j-th column of the matrix B.

As an example of the application of this rule, we present the formula for multiplying square matrices of the second order.

× =

Formula (1.4) implies the following properties of the matrix product A on the matrix IN:

1) associative property: (A B) C = A (B C);

2) distributive property with respect to the sum of matrices:

(A + B) C = A C + B C or A (B + C) = A B + A C.

The question of the permutation (commutative) property of the product of a matrix A to matrix IN it makes sense to set only for square matrices A and B the same order.

We present important special cases of matrices for which the permutation property is also valid. Two matrices for the product of which the permutation property is valid are usually called commuting.

Among square matrices, we single out a class of so-called diagonal matrices, each of which has elements located outside the main diagonal equal to zero. Each diagonal matrix of order P has the form

D= (1.5)

Where d1, d2,… ,dn-any number. It is easy to see that if all these numbers are equal to each other, i.e. d1=d2=… = d n then for any square matrix A order P fair equality A D = D A.

Among all diagonal matrices (1.5) with coinciding entries d1=d2=… = d n = = d two matrices play a particularly important role. The first of these matrices is obtained by d=1 is called the identity matrix n E. The second matrix is ​​obtained with d=0, is called the null matrix n th order and is denoted by the symbol Oh Thus,

E= O=

By virtue of what was proved above A E = E A And A O = O A. Moreover, it is easy to show that

A E \u003d E A \u003d A, A O \u003d O A \u003d 0. (1.6)

The first of formulas (1.6) characterizes the special role of the identity matrix E, similar to the role played by the number 1 in multiplication of real numbers. As for the special role of the zero matrix ABOUT, then it is revealed not only by the second of formulas (1.7), but also by the elementarily verifiable equality

A + 0 = 0 + A = A.

In conclusion, we note that the concept of a zero matrix can also be introduced for non-square matrices (zero is called any matrix, all elements of which are equal to zero).

Block matrices

Suppose some matrix A = || a ij || using horizontal and vertical lines, it is divided into separate rectangular cells, each of which is a matrix of smaller sizes and is called a block of the original matrix. In this case, it becomes possible to consider the original matrix A as some new (so-called block) matrix A = || A a b ||, whose elements are the specified blocks. We designate these elements with a capital Latin letter to emphasize that they are, generally speaking, matrices, not numbers, and (like ordinary numeric elements) we supply two indices, the first of which indicates the number of the "block" row, and the second - the number of the "block" row. » column.

For example, matrix

can be viewed as a block matrix

the elements of which are the following blocks:

Remarkable is the fact that the basic operations with block matrices are performed according to the same rules by which they are performed with ordinary numerical matrices, only blocks act as elements.

The concept of a determinant.

Consider an arbitrary square matrix of any order P:

A= (1.7)

With each such matrix, we associate a well-defined numerical characteristic, called the determinant corresponding to this matrix.

If order n matrix (1.7) is equal to one, then this matrix consists of one element a i j is the first-order determinant corresponding to such a matrix, we will call the value of this element.

then the second-order determinant corresponding to such a matrix is ​​the number equal to a 11 a 22 - a 12 a 21 and denoted by one of the symbols:

So by definition

(1.9)

Formula (1.9) is a rule for compiling a second-order determinant from the elements of the matrix corresponding to it. The verbal formulation of this rule is as follows: the second-order determinant corresponding to matrix (1.8) is equal to the difference between the product of the elements on the main diagonal of this matrix and the product of the elements on its secondary diagonal. Determinants of the second and higher orders are widely used in solving systems of linear equations.

Let's see how it works operations with matrices in the MathCad system . The simplest matrix algebra operations are implemented in MathCad as operators. Writing operators in terms of meaning is as close as possible to their mathematical action. Each operator is expressed by a corresponding symbol. Consider the matrix and vector operations of MathCad 2001. Vectors are a special case of matrices of dimension n x 1, therefore, all the same operations are valid for them as for matrices, unless restrictions are specifically specified (for example, some operations are applicable only to square matrices n x n). Some actions are valid only for vectors (for example, the scalar product), and some, despite the same spelling, act differently on vectors and matrices.

In the dialog that appears, set the number of rows and columns of the matrix.

q After pressing the OK button, a field for entering matrix elements opens. To enter a matrix element, place the cursor in the marked position and enter a number or expression from the keyboard.

In order to perform any operation using the toolbar, you need to:

q select the matrix and click on the operation button in the panel,

q or click on the button in the panel and enter the name of the matrix in the marked position.

The “Symbols” menu contains three operations - transpose, invert, determinant.

This means, for example, that you can calculate the matrix determinant by executing the command Symbols/Matrices/Determinant.

The number of the first row (and the first column) of the MathCAD matrix is ​​stored in the ORIGIN variable. By default, the countdown is from zero. In mathematical notation, it is more common to count from 1. In order for MathCAD to count row and column numbers from 1, you need to set the variable ORIGIN:=1.

Functions intended for working with linear algebra problems are collected in the “Vectors and Matrices” section of the “Insert Function” dialog (we remind you that it is called by the button on the “Standard” panel). The main of these functions will be described later.

Transposition

Fig.2 Matrix transposition

In MathCAD, you can both add matrices and subtract them from each other. These operators use the symbols <+> or <-> respectively. The matrices must have the same dimension, otherwise an error message will be generated. Each element of the sum of two matrices is equal to the sum of the corresponding elements of the matrix terms (example in Fig. 3).
In addition to matrix addition, MathCAD supports the addition of a matrix with a scalar value, i.e. number (example in Fig. 4). Each element of the resulting matrix is ​​equal to the sum of the corresponding element of the original matrix and a scalar value.
To enter the multiplication symbol, you need to press the asterisk key<*>or use the toolbar Matrix (Matrix), pressing the button on it Dot Product (Multiply)(Fig. 1). Matrix multiplication is denoted by default with a dot, as shown in the example in Figure 6. The symbol for matrix multiplication can be chosen in the same way as in scalar expressions.
Another example related to the multiplication of a vector by a row matrix and, conversely, a row by a vector, is shown in Fig. 7. The second line of this example shows how the formula looks like when you choose to display the multiplication operator No Space (Together). However, the same multiplication operator acts differently on two vectors. .

Similar information.

Service assignment. Matrix Calculator designed to solve matrix expressions such as 3A-CB 2 or A -1 +B T .

Instruction. For an online solution, you must specify a matrix expression. At the second stage, it will be necessary to clarify the dimensions of the matrices.

Matrix Actions

Valid operations: multiplication (*), addition (+), subtraction (-), matrix inverse A^(-1) , exponentiation (A^2 , B^3), matrix transposition (A^T).

Valid operations: multiplication (*), addition (+), subtraction (-), matrix inverse A^(-1) , exponentiation (A^2 , B^3), matrix transposition (A^T).
To perform a list of operations, use the semicolon (;) separator. For example, to perform three operations:
a) 3A + 4B
b) AB-BA
c) (A-B) -1
will need to be written like this: 3*A+4*B;A*B-B*A;(A-B)^(-1)

A matrix is ​​a rectangular numerical table with m rows and n columns, so the matrix can be schematically represented as a rectangle.
Zero matrix (null matrix) is called a matrix, all elements of which are equal to zero and denote 0.
identity matrix is called a square matrix of the form

Two matrices A and B are equal if they are the same size and their corresponding elements are equal.
Singular matrix is called a matrix whose determinant is equal to zero (Δ = 0).

Let's define basic operations on matrices.

Matrix addition

Definition . The sum of two matrices of the same size is a matrix of the same dimensions, the elements of which are found by the formula . Denoted C = A+B.

Example 6 . .
The operation of matrix addition extends to the case of any number of terms. Obviously, A+0=A .
We emphasize once again that only matrices of the same size can be added; for matrices of different sizes, the addition operation is not defined.

Matrix subtraction

Definition . The difference B-A of matrices B and A of the same size is a matrix C such that A + C = B.

Matrix multiplication

Definition . The product of a matrix by a number α is the matrix obtained from A by multiplying all its elements by α, .
Definition . Let two matrices be given and , and the number of columns A is equal to the number of rows B. The product of A by B is a matrix whose elements are found by the formula .
Denoted C = A B.
Schematically, the operation of matrix multiplication can be depicted as follows:

and the rule for calculating an element in a product:

Let us emphasize once again that the product A B makes sense if and only if the number of columns of the first factor is equal to the number of rows of the second, while the product produces a matrix whose number of rows is equal to the number of rows of the first factor, and the number of columns is equal to the number of columns of the second. You can check the result of multiplication through a special online calculator.

Example 7 . Matrix data And . Find the matrices C = A·B and D = B·A.
Solution. First of all, note that the product A B exists because the number of columns in A is equal to the number of rows in B.

Note that in the general case A·B≠B·A , i.e. the product of matrices is anticommutative.
Let's find B·A (multiplication is possible).

Example 8 . Given a matrix . Find 3A 2 - 2A.
Solution.

.
; .
.
We note the following curious fact.
As you know, the product of two non-zero numbers is not equal to zero. For matrices, such a circumstance may not take place, that is, the product of nonzero matrices may turn out to be equal to the zero matrix.

Matrix, get acquainted with its basic concepts. The defining elements of the matrix are its diagonals - and side. The main one starts from the element in the first row, first column and continues to the element of the last column, last row (that is, it goes from left to right). The side diagonal starts vice versa in the first row, but the last column and continues to the element that has the coordinates of the first column and the last row (goes from right to left).

In order to move on to the next definitions and algebraic operations with matrices, study the types of matrices. The simplest of them are square, unit, zero and inverse. In the same number of columns and rows. The transposed matrix, let's call it B, is obtained from matrix A by replacing columns with rows. In the unit, all elements of the main diagonal are ones, and the others are zeros. And in zero, even the elements of the diagonals are zero. The inverse matrix is ​​the one on which the original matrix comes to the identity form.

Also, the matrix can be symmetrical about the main or side axes. That is, the element having coordinates a(1;2), where 1 is the row number and 2 is the column number, is equal to a(2;1). A(3;1)=A(1;3) and so on. Matched matrices are those where the number of columns of one is equal to the number of rows of the other (such matrices can be multiplied).

The main actions that can be performed with matrices are addition, multiplication and finding the determinant. If the matrices are the same size, that is, they have an equal number of rows and columns, then they can be added. It is necessary to add the elements that are in the same places in the matrices, that is, add a (m; n) with in (m; n), where m and n are the corresponding column and row coordinates. When adding matrices, the main rule of ordinary arithmetic addition applies - when the places of the terms are changed, the sum does not change. Thus, if instead of a simple element a there is an expression a + b, then it can be added to an element from another commensurate matrix according to the rules a + (b + c) \u003d (a + c) + c.

You can multiply consistent matrices, which are given above. In this case, a matrix is ​​obtained, where each element is the sum of the pairwise multiplied elements of the row of the matrix A and the column of the matrix B. When multiplying, the order of operations is very important. m*n is not equal to n*m.

Also, one of the main actions is finding. It is also called a determinant and is designated as follows: det. This value is determined modulo, that is, it is never negative. The easiest way to find the determinant is for a square 2x2 matrix. To do this, you need to multiply the elements of the main diagonal and subtract from them the multiplied elements of the secondary diagonal.

DEFINITION OF A MATRIX. TYPES OF MATRIXES

Matrix size m× n is called the totality m n numbers arranged in a rectangular table of m lines and n columns. This table is usually enclosed in parentheses. For example, the matrix might look like:

For brevity, the matrix can be denoted by a single capital letter, for example, A or IN.

In general, a matrix of size m× n write like this

.

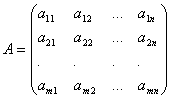The numbers that make up a matrix are called matrix elements. It is convenient to supply matrix elements with two indices aij: The first indicates the row number and the second indicates the column number. For example, a 23– the element is in the 2nd row, 3rd column.

If the number of rows in a matrix is ​​equal to the number of columns, then the matrix is ​​called square, and the number of its rows or columns is called in order matrices. In the examples above, the second matrix is ​​square - its order is 3, and the fourth matrix - its order is 1.

A matrix in which the number of rows is not equal to the number of columns is called rectangular. In the examples, this is the first matrix and the third.

There are also matrices that have only one row or one column.

A matrix with only one row is called matrix - row(or string), and a matrix that has only one column, matrix - column.

A matrix in which all elements are equal to zero is called null and is denoted by (0), or simply 0. For example,

.

main diagonal A square matrix is ​​the diagonal going from the upper left to the lower right corner.

A square matrix in which all elements below the main diagonal are equal to zero is called triangular matrix.

.

A square matrix in which all elements, except perhaps those on the main diagonal, are equal to zero, is called diagonal matrix. For example, or.

A diagonal matrix in which all diagonal entries are equal to one is called single matrix and is denoted by the letter E. For example, the 3rd order identity matrix has the form .

ACTIONS ON MATRIXES

Matrix equality. Two matrices A And B are said to be equal if they have the same number of rows and columns and their corresponding elements are equal aij = b ij. So if And , That A=B, If a 11 = b 11, a 12 = b 12, a 21 = b 21 And a 22 = b 22.

Transposition. Consider an arbitrary matrix A from m lines and n columns. It can be associated with the following matrix B from n lines and m columns, where each row is a column of the matrix A with the same number (hence each column is a row of the matrix A with the same number). So if , That .

This matrix B called transposed matrix A, and the transition from A To B transposition.

Thus, transposition is a reversal of the roles of rows and columns of a matrix. Matrix transposed to matrix A, usually denoted A T.

Communication between the matrix A and its transposed can be written as .

For example. Find the matrix transposed to the given one.

Matrix addition. Let matrices A And B consist of the same number of rows and the same number of columns, i.e. have same sizes. Then in order to add the matrices A And B need to matrix elements A add matrix elements B standing in the same places. Thus, the sum of two matrices A And B called matrix C, which is determined by the rule, for example,

Examples. Find the sum of matrices:

It is easy to check that matrix addition obeys the following laws: commutative A+B=B+A and associative ( A+B)+C=A+(B+C).

Multiplying a matrix by a number. To multiply a matrix A per number k need each element of the matrix A multiply by that number. So the matrix product A per number k there is a new matrix, which is determined by the rule or .

For any numbers a And b and matrices A And B equalities are fulfilled:

Examples.

Matrix multiplication. This operation is carried out according to a peculiar law. First of all, we note that the sizes of the matrix factors must be consistent. You can multiply only those matrices whose number of columns of the first matrix matches the number of rows of the second matrix (i.e. the length of the first row is equal to the height of the second column). work matrices A not a matrix B called the new matrix C=AB, whose elements are composed as follows:

Thus, for example, in order to get the product (i.e., in the matrix C) the element in the 1st row and 3rd column from 13, you need to take the 1st row in the 1st matrix, the 3rd column in the 2nd, and then multiply the row elements by the corresponding column elements and add the resulting products. And other elements of the product matrix are obtained using a similar product of the rows of the first matrix by the columns of the second matrix.

In general, if we multiply the matrix A = (aij) size m× n to matrix B = (bij) size n× p, then we get the matrix C size m× p, whose elements are calculated as follows: element c ij is obtained as a result of the product of elements i th row of the matrix A on the relevant elements j-th column of the matrix B and their summation.

From this rule it follows that you can always multiply two square matrices of the same order, as a result we get a square matrix of the same order. In particular, a square matrix can always be multiplied by itself, i.e. square up.

Another important case is the multiplication of a matrix-row by a matrix-column, and the width of the first must be equal to the height of the second, as a result we get a matrix of the first order (i.e. one element). Really,

.

Examples.

Thus, these simple examples show that matrices, generally speaking, do not commute with each other, i.e. A∙B ≠ B∙A . Therefore, when multiplying matrices, you need to carefully monitor the order of the factors.

It can be verified that matrix multiplication obeys the associative and distributive laws, i.e. (AB)C=A(BC) And (A+B)C=AC+BC.

It is also easy to check that when multiplying a square matrix A to the identity matrix E of the same order, we again obtain the matrix A, moreover AE=EA=A.

The following curious fact may be noted. As is known, the product of 2 non-zero numbers is not equal to 0. For matrices, this may not be the case; the product of 2 non-zero matrices may be equal to the zero matrix.

For example, If , That

.

THE CONCEPT OF DETERMINERS

Let a second-order matrix be given - a square matrix consisting of two rows and two columns .

Second order determinant corresponding to this matrix is ​​the number obtained as follows: a 11 a 22 – a 12 a 21.

The determinant is denoted by the symbol .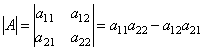

So, in order to find the second-order determinant, you need to subtract the product of the elements along the second diagonal from the product of the elements of the main diagonal.

Examples. Calculate second order determinants.

Similarly, we can consider a matrix of the third order and the corresponding determinant.

Third order determinant, corresponding to a given square matrix of the third order, is a number denoted and obtained as follows:

.

Thus, this formula gives the expansion of the third order determinant in terms of the elements of the first row a 11 , a 12 , a 13 and reduces the calculation of the third order determinant to the calculation of second order determinants.

Examples. Calculate the third order determinant.

Similarly, one can introduce the concepts of determinants of the fourth, fifth, etc. orders, lowering their order by expansion over the elements of the 1st row, while the signs "+" and "-" for the terms alternate.

So, unlike the matrix, which is a table of numbers, the determinant is a number that is assigned in a certain way to the matrix.

This topic will cover operations such as addition and subtraction of matrices, multiplication of a matrix by a number, multiplication of a matrix by a matrix, matrix transposition. All symbols used on this page are taken from the previous topic.

Addition and subtraction of matrices.

The sum $A+B$ of the matrices $A_(m\times n)=(a_(ij))$ and $B_(m\times n)=(b_(ij))$ is the matrix $C_(m\times n) =(c_(ij))$, where $c_(ij)=a_(ij)+b_(ij)$ for all $i=\overline(1,m)$ and $j=\overline(1,n) $.

A similar definition is introduced for the difference of matrices:

The difference $A-B$ of the matrices $A_(m\times n)=(a_(ij))$ and $B_(m\times n)=(b_(ij))$ is the matrix $C_(m\times n)=( c_(ij))$, where $c_(ij)=a_(ij)-b_(ij)$ for all $i=\overline(1,m)$ and $j=\overline(1,n)$.

Explanation for the entry $i=\overline(1,m)$: show\hide

The entry "$i=\overline(1,m)$" means that the parameter $i$ changes from 1 to m. For example, the entry $i=\overline(1,5)$ says that the $i$ parameter takes the values ​​1, 2, 3, 4, 5.

It is worth noting that addition and subtraction operations are defined only for matrices of the same size. In general, the addition and subtraction of matrices are operations that are intuitively clear, because they mean, in fact, just the summation or subtraction of the corresponding elements.

Example #1

Three matrices are given:

$$ A=\left(\begin(array) (ccc) -1 & -2 & 1 \\ 5 & 9 & -8 \end(array) \right)\;\; B=\left(\begin(array) (ccc) 10 & -25 & 98 \\ 3 & 0 & -14 \end(array) \right); \;\; F=\left(\begin(array) (cc) 1 & 0 \\ -5 & 4 \end(array) \right). $$

Is it possible to find the matrix $A+F$? Find matrices $C$ and $D$ if $C=A+B$ and $D=A-B$.

Matrix $A$ contains 2 rows and 3 columns (in other words, the size of matrix $A$ is $2\times 3$), and matrix $F$ contains 2 rows and 2 columns. The dimensions of the matrix $A$ and $F$ do not match, so we cannot add them, i.e. the operation $A+F$ for these matrices is not defined.

The sizes of the matrices $A$ and $B$ are the same, i.e. matrix data contains an equal number of rows and columns, so the addition operation is applicable to them.

$$ C=A+B=\left(\begin(array) (ccc) -1 & -2 & 1 \\ 5 & 9 & -8 \end(array) \right)+ \left(\begin(array ) (ccc) 10 & -25 & 98 \\ 3 & 0 & -14 \end(array) \right)=\\= \left(\begin(array) (ccc) -1+10 & -2+( -25) & 1+98 \\ 5+3 & 9+0 & -8+(-14) \end(array) \right)= \left(\begin(array) (ccc) 9 & -27 & 99 \\ 8 & 9 & -22 \end(array) \right) $$

Find the matrix $D=A-B$:

$$ D=A-B=\left(\begin(array) (ccc) -1 & -2 & 1 \\ 5 & 9 & -8 \end(array) \right)- \left(\begin(array) ( ccc) 10 & -25 & 98 \\ 3 & 0 & -14 \end(array) \right)=\\= \left(\begin(array) (ccc) -1-10 & -2-(-25 ) & 1-98 \\ 5-3 & 9-0 & -8-(-14) \end(array) \right)= \left(\begin(array) (ccc) -11 & 23 & -97 \ \ 2 & 9 & 6 \end(array) \right) $$

Answer: $C=\left(\begin(array) (ccc) 9 & -27 & 99 \\ 8 & 9 & -22 \end(array) \right)$, $D=\left(\begin(array) (ccc) -11 & 23 & -97 \\ 2 & 9 & 6 \end(array) \right)$.

Multiplying a matrix by a number.

The product of the matrix $A_(m\times n)=(a_(ij))$ and the number $\alpha$ is the matrix $B_(m\times n)=(b_(ij))$, where $b_(ij)= \alpha\cdot a_(ij)$ for all $i=\overline(1,m)$ and $j=\overline(1,n)$.

Simply put, to multiply a matrix by some number means to multiply each element of the given matrix by that number.

Example #2

Given a matrix: $ A=\left(\begin(array) (ccc) -1 & -2 & 7 \\ 4 & 9 & 0 \end(array) \right)$. Find matrices $3\cdot A$, $-5\cdot A$ and $-A$.

$$ 3\cdot A=3\cdot \left(\begin(array) (ccc) -1 & -2 & 7 \\ 4 & 9 & 0 \end(array) \right) =\left(\begin( array) (ccc) 3\cdot(-1) & 3\cdot(-2) & 3\cdot 7 \\ 3\cdot 4 & 3\cdot 9 & 3\cdot 0 \end(array) \right)= \left(\begin(array) (ccc) -3 & -6 & 21 \\ 12& 27 & 0 \end(array) \right).\\ -5\cdot A=-5\cdot \left(\begin (array) (ccc) -1 & -2 & 7 \\ 4 & 9 & 0 \end(array) \right) =\left(\begin(array) (ccc) -5\cdot(-1) & - 5\cdot(-2) & -5\cdot 7 \\ -5\cdot 4 & -5\cdot 9 & -5\cdot 0 \end(array) \right)= \left(\begin(array) ( ccc) 5 & 10 & -35 \\ -20 & -45 & 0 \end(array) \right). $$

The notation $-A$ is shorthand for $-1\cdot A$. That is, to find $-A$, you need to multiply all the elements of the $A$ matrix by (-1). In fact, this means that the sign of all elements of the matrix $A$ will change to the opposite:

$$ -A=-1\cdot A=-1\cdot \left(\begin(array) (ccc) -1 & -2 & 7 \\ 4 & 9 & 0 \end(array) \right)= \ left(\begin(array) (ccc) 1 & 2 & -7 \\ -4 & -9 & 0 \end(array) \right) $$

Answer: $3\cdot A=\left(\begin(array) (ccc) -3 & -6 & 21 \\ 12& 27 & 0 \end(array) \right);\; -5\cdot A=\left(\begin(array) (ccc) 5 & 10 & -35 \\ -20 & -45 & 0 \end(array) \right);\; -A=\left(\begin(array) (ccc) 1 & 2 & -7 \\ -4 & -9 & 0 \end(array) \right)$.

The product of two matrices.

The definition of this operation is cumbersome and, at first glance, incomprehensible. Therefore, I will first indicate a general definition, and then we will analyze in detail what it means and how to work with it.

The product of the matrix $A_(m\times n)=(a_(ij))$ and the matrix $B_(n\times k)=(b_(ij))$ is the matrix $C_(m\times k)=(c_( ij))$, for which each element of $c_(ij)$ is equal to the sum of the products of the corresponding elements of the i-th row of the matrix $A$ and the elements of the j-th column of the matrix $B$: $$c_(ij)=\sum\limits_ (p=1)^(n)a_(ip)b_(pj), \;\; i=\overline(1,m), j=\overline(1,n).$$

Step by step, we will analyze the multiplication of matrices using an example. However, you should immediately pay attention that not all matrices can be multiplied. If we want to multiply matrix $A$ by matrix $B$, then first we need to make sure that the number of columns of matrix $A$ is equal to the number of rows of matrix $B$ (such matrices are often called agreed). For example, matrix $A_(5\times 4)$ (matrix contains 5 rows and 4 columns) cannot be multiplied by matrix $F_(9\times 8)$ (9 rows and 8 columns), since the number of columns of matrix $A $ is not equal to the number of rows of matrix $F$, i.e. $4\neq 9$. But it is possible to multiply the matrix $A_(5\times 4)$ by the matrix $B_(4\times 9)$, since the number of columns of the matrix $A$ is equal to the number of rows of the matrix $B$. In this case, the result of multiplying the matrices $A_(5\times 4)$ and $B_(4\times 9)$ is the matrix $C_(5\times 9)$, containing 5 rows and 9 columns:

Example #3

Given matrices: $ A=\left(\begin(array) (cccc) -1 & 2 & -3 & 0 \\ 5 & 4 & -2 & 1 \\ -8 & 11 & -10 & -5 \end (array) \right)$ and $ B=\left(\begin(array) (cc) -9 & 3 \\ 6 & 20 \\ 7 & 0 \\ 12 & -4 \end(array) \right) $. Find the matrix $C=A\cdot B$.

To begin with, we immediately determine the size of the matrix $C$. Since matrix $A$ has size $3\times 4$ and matrix $B$ has size $4\times 2$, the size of matrix $C$ is $3\times 2$:

So, as a result of the product of the matrices $A$ and $B$, we should get the matrix $C$, consisting of three rows and two columns: $ C=\left(\begin(array) (cc) c_(11) & c_( 12) \\ c_(21) & c_(22) \\ c_(31) & c_(32) \end(array) \right)$. If the designations of the elements raise questions, then you can look at the previous topic: "Matrices. Types of matrices. Basic terms", at the beginning of which the designation of the matrix elements is explained. Our goal is to find the values ​​of all elements of the matrix $C$.

Let's start with the element $c_(11)$. To get the element $c_(11)$, you need to find the sum of the products of the elements of the first row of the matrix $A$ and the first column of the matrix $B$:

To find the element $c_(11)$ itself, you need to multiply the elements of the first row of the matrix $A$ by the corresponding elements of the first column of the matrix $B$, i.e. the first element to the first, the second to the second, the third to the third, the fourth to the fourth. We summarize the results obtained:

$$ c_(11)=-1\cdot (-9)+2\cdot 6+(-3)\cdot 7 + 0\cdot 12=0. $$

Let's continue the solution and find $c_(12)$. To do this, you have to multiply the elements of the first row of the matrix $A$ and the second column of the matrix $B$:

Similarly to the previous one, we have:

$$ c_(12)=-1\cdot 3+2\cdot 20+(-3)\cdot 0 + 0\cdot (-4)=37. $$

All elements of the first row of the matrix $C$ are found. We pass to the second line, which begins with the element $c_(21)$. To find it, you have to multiply the elements of the second row of the matrix $A$ and the first column of the matrix $B$:

$$ c_(21)=5\cdot (-9)+4\cdot 6+(-2)\cdot 7 + 1\cdot 12=-23. $$

The next element $c_(22)$ is found by multiplying the elements of the second row of the matrix $A$ by the corresponding elements of the second column of the matrix $B$:

$$ c_(22)=5\cdot 3+4\cdot 20+(-2)\cdot 0 + 1\cdot (-4)=91. $$

To find $c_(31)$ we multiply the elements of the third row of the matrix $A$ by the elements of the first column of the matrix $B$:

$$ c_(31)=-8\cdot (-9)+11\cdot 6+(-10)\cdot 7 + (-5)\cdot 12=8. $$

And, finally, to find the element $c_(32)$, you have to multiply the elements of the third row of the matrix $A$ by the corresponding elements of the second column of the matrix $B$:

$$ c_(32)=-8\cdot 3+11\cdot 20+(-10)\cdot 0 + (-5)\cdot (-4)=216. $$

All elements of the matrix $C$ are found, it remains only to write down that $C=\left(\begin(array) (cc) 0 & 37 \\ -23 & 91 \\ 8 & 216 \end(array) \right)$ . Or, to write it in full:

$$ C=A\cdot B =\left(\begin(array) (cccc) -1 & 2 & -3 & 0 \\ 5 & 4 & -2 & 1 \\ -8 & 11 & -10 & - 5 \end(array) \right)\cdot \left(\begin(array) (cc) -9 & 3 \\ 6 & 20 \\ 7 & 0 \\ 12 & -4 \end(array) \right) =\left(\begin(array) (cc) 0 & 37 \\ -23 & 91 \\ 8 & 216 \end(array) \right). $$

Answer: $C=\left(\begin(array) (cc) 0 & 37 \\ -23 & 91 \\ 8 & 216 \end(array) \right)$.

By the way, there is often no reason to describe in detail the location of each element of the result matrix. For matrices, the size of which is small, you can do the following:

It is also worth noting that matrix multiplication is non-commutative. This means that in general $A\cdot B\neq B\cdot A$. Only for some types of matrices, which are called permutational(or commuting), the equality $A\cdot B=B\cdot A$ is true. It is on the basis of the non-commutativity of multiplication that it is required to indicate exactly how we multiply the expression by one or another matrix: on the right or on the left. For example, the phrase "multiply both sides of the equality $3E-F=Y$ by the matrix $A$ on the right" means that you want to get the following equality: $(3E-F)\cdot A=Y\cdot A$.

Transposed with respect to the matrix $A_(m\times n)=(a_(ij))$ is the matrix $A_(n\times m)^(T)=(a_(ij)^(T))$, for elements where $a_(ij)^(T)=a_(ji)$.

Simply put, in order to get the transposed matrix $A^T$, you need to replace the columns in the original matrix $A$ with the corresponding rows according to this principle: there was the first row - the first column will become; there was a second row - the second column will become; there was a third row - there will be a third column and so on. For example, let's find the transposed matrix to the matrix $A_(3\times 5)$:

Accordingly, if the original matrix had size $3\times 5$, then the transposed matrix has size $5\times 3$.

Some properties of operations on matrices.

It is assumed here that $\alpha$, $\beta$ are some numbers, and $A$, $B$, $C$ are matrices. For the first four properties, I indicated the names, the rest can be named by analogy with the first four.

1. $A+B=B+A$ (commutativity of addition)
2. $A+(B+C)=(A+B)+C$ (addition associativity)
3. $(\alpha+\beta)\cdot A=\alpha A+\beta A$ (distributivity of multiplication by a matrix with respect to addition of numbers)
4. $\alpha\cdot(A+B)=\alpha A+\alpha B$ (distributivity of multiplication by a number with respect to matrix addition)
5. $A(BC)=(AB)C$
6. $(\alpha\beta)A=\alpha(\beta A)$
7. $A\cdot (B+C)=AB+AC$, $(B+C)\cdot A=BA+CA$.
8. $A\cdot E=A$, $E\cdot A=A$, where $E$ is the identity matrix of the corresponding order.
9. $A\cdot O=O$, $O\cdot A=O$, where $O$ is a zero matrix of the corresponding size.
10. $\left(A^T \right)^T=A$
11. $(A+B)^T=A^T+B^T$
12. $(AB)^T=B^T\cdot A^T$
13. $\left(\alpha A \right)^T=\alpha A^T$

In the next part, the operation of raising a matrix to a non-negative integer power will be considered, and examples will be solved in which several operations on matrices will be required.