Equations with two variables are examples. Equations with two variables
Solving equations in integers is one of the oldest mathematical problems. Already at the beginning of the 2nd millennium BC. e. The Babylonians knew how to solve systems of such equations with two variables. This area of mathematics reached its greatest prosperity in ancient Greece. The main source for us is the "Arithmetic" of Diophantus, which contains various types of equations. In it, Diophantus (after his name and the name of the equations - Diophantine equations) anticipates a number of methods for studying equations of the 2nd and 3rd degrees, which developed only in the 19th century.
The simplest Diophantine equations ax + y = 1 (equation with two variables, first degree) x2 + y2 = z2 (equation with three variables, second degree)
Algebraic equations have been studied most fully; their solution was one of the most important problems in algebra in the 16th and 17th centuries.
By the beginning of the 19th century, the works of P. Fermat, L. Euler, K. Gauss investigated a Diophantine equation of the form: ax2 + bxy + cy2 + dx + ey + f = 0, where a, b, c, d, e, f are numbers; x, y are unknown variables.
This is a 2nd degree equation with two unknowns.
K. Gauss built a general theory of quadratic forms, which is the basis for solving certain types of equations with two variables (Diophantine equations). There are a large number of specific Diophantine equations that can be solved by elementary methods. /p>
theoretical material.
In this part of the work, the basic mathematical concepts will be described, the definitions of terms will be given, the decomposition theorem will be formulated using the method of indefinite coefficients, which were studied and considered when solving equations with two variables.
Definition 1: An equation of the form ax2 + bxy + cy2 + dx + ey + f = 0, where a, b, c, d, e, f are numbers; x, y unknown variables is called a second-degree equation with two variables.
In the school course of mathematics, the quadratic equation ax2 + inx + c \u003d 0 is studied, where a, b, c of the number x is a variable, with one variable. There are many ways to solve such an equation:
1. Finding roots using the discriminant;
2. Finding roots for an even coefficient in (according to D1 =);
3. Finding roots by Vieta's theorem;
4. Finding the roots using the selection of the full square of the binomial.
Solving an equation means finding all its roots or proving that there are none.
Definition 2: The root of an equation is a number that, when substituted into the equation, forms a true equality.
Definition 3: The solution of an equation with two variables is called a pair of numbers (x, y), when substituting them into the equation, it turns into a true equality.
The process of searching for solutions to an equation very often usually consists in replacing the equation with an equivalent equation, but simpler in solution. Such equations are called equivalent.
Definition 4: Two equations are said to be equivalent if each solution to one equation is a solution to the other equation, and vice versa, and both equations are considered in the same area.
To solve equations with two variables, the theorem on the expansion of the equation into a sum of perfect squares is used (by the method of indefinite coefficients).
For the second order equation ax2 + bxy + cy2 + dx + ey + f = 0 (1) there is a decomposition a(x + py + q)2 + r(y + s)2 + h (2)
Let us formulate the conditions under which expansion (2) takes place for equation (1) of two variables.
Theorem: If the coefficients a, c, c of equation (1) satisfy the conditions a0 and 4av - c20, then expansion (2) is determined in a unique way.
In other words, equation (1) with two variables can be reduced to the form (2) using the method of indefinite coefficients, if the conditions of the theorem are satisfied.
Let's look at an example of how the method of indefinite coefficients is implemented.
METHOD #1. Solve the equation by the method of indeterminate coefficients
2 x2 + y2 + 2xy + 2x + 1 = 0.
1. Let's check the fulfillment of the conditions of the theorem, a=2, b=1, c=2, so a=2,4av - c2= 4∙2∙1- 22= 40.
2. The conditions of the theorem are satisfied, and can be expanded by formula (2).
3. 2 x2 + y2 + 2xy + 2x + 1 = 2(x + py + q)2 + r(y + s)2 + h, based on the conditions of the theorem, both parts of the identity are equivalent. Simplify the right side of the identity.
4. 2(x + py + q)2 + r(y +s)2 +h =
2(x2 + p2y2 + q2 + 2pxy + 2pqy + 2qx) + r(y2 + 2sy + s2) + h =
2x2+ 2p2y2 + 2q2 + 4pxy + 4pqy + 4qx + ry2 + 2rsy + rs2 + h =
X2(2) + y2(2p2 + r) + xy(4p) + x(4q) + y(4pq + 2rs) + (2q2 + rs2 + h).
5. Equate the coefficients for the same variables with their powers.
x2 2 = 2 y21 = 2p2 + r) xy2 = 4p x2 = 4q y0 = 4pq + 2rs x01 = 2q2 + rs2 + h
6. Get a system of equations, solve it and find the values of the coefficients.
7. Substitute the coefficients in (2), then the equation will take the form
2 x2 + y2 + 2xy + 2x + 1 \u003d 2 (x + 0.5y + 0.5) 2 + 0.5 (y -1) 2 + 0
Thus, the original equation is equivalent to the equation
2(x + 0.5y + 0.5)2 + 0.5(y -1)2 = 0 (3), this equation is equivalent to a system of two linear equations.
Answer: (-1; 1).
If you pay attention to the type of decomposition (3), you can see that it is identical in form to the extraction of a full square from a quadratic equation with one variable: ax2 + inx + c = a(x +)2 +.
Let's apply this trick to solving an equation with two variables. Let's solve with the help of selection of a full square the quadratic equation with two variables already solved using the theorem.
METHOD #2: Solve the equation 2x2 + y2 + 2xy + 2x +1= 0.
Solution: 1. We represent 2x2 as the sum of two terms x2 + x2 + y2 + 2xy + 2x + 1 = 0.
2. We group the terms in such a way that we can collapse according to the full square formula.
(x2 + y2 + 2xy) + (x2 + 2x + 1) = 0.
3. Select the full squares from the expressions in brackets.
(x + y)2 + (x + 1)2 = 0.
4. This equation is equivalent to a system of linear equations.
Answer: (-1;1).
If we compare the results, we can see that the equation solved by method No. 1 using the theorem and the method of indefinite coefficients and the equation solved by method No. 2 using the selection of a full square have the same roots.
Conclusion: A quadratic equation with two variables can be expanded into a sum of squares in two ways:
➢ The first method is the method of indeterminate coefficients, which is based on the theorem and expansion (2).
➢ The second way is with the help of identical transformations, which make it possible to select consecutively complete squares.
Of course, when solving problems, the second method is preferable, since it does not require memorizing expansion (2) and conditions.
This method can also be applied to quadratic equations with three variables. The selection of the full square in such equations is more laborious. I will be doing this kind of transformation next year.
It is interesting to note that a function having the form f(x, y)= ax2 + bxy + cy2 + dx + ey + f is called a quadratic function of two variables. Quadratic functions play an important role in various branches of mathematics:
In mathematical programming (quadratic programming)
In linear algebra and geometry (quadratic forms)
In the theory of differential equations (reducing a second-order linear equation to a canonical form).
When solving these various problems, one has, in fact, to apply the procedure for extracting the full square from a quadratic equation (one, two or more variables).
Lines whose equations are described by a quadratic equation of two variables are called curves of the second order.
This circle, ellipse, hyperbola.
When plotting these curves, the method of successive selection of the full square is also used.
Let's consider how the method of successive selection of a full square works on specific examples.
Practical part.
Solve equations using the method of successive selection of the full square.
1. 2x2 + y2 + 2xy + 2x + 1 = 0; x2 + x2 + y2 + 2xy + 2x + 1 = 0;
(x + 1)2 + (x + y)2 = 0;
Answer: (-1; 1).
2. x2 + 5y2 + 2xy + 4y + 1 = 0; x2 + 4y2 + y2 + 2xy + 4y + 1 = 0;
(x + y)2 + (2y + 1)2 = 0;
Answer: (0.5; - 0.5).
3. 3x2 + 4y2 - 6xy - 2y + 1 = 0;
3x2 + 3y2 + y2 - 6xy - 2y +1 = 0;
3x2 + 3y2 - 6xy + y2 -2y +1 = 0;
3(x2 - 2xy + y2) + y2 - 2y + 1 = 0;
3(x2 - 2xy + y2)+(y2 - 2y + 1)=0;
3(x-y)2 + (y-1)2 = 0;
Answer: (-1; 1).
Solve Equations:
1. 2x2 + 3y2 - 4xy + 6y +9 = 0
(bring to the form: 2(x-y)2 + (y +3)2 = 0)
Answer: (-3; -3)
2. - 3x2 - 2y2 - 6xy -2y + 1=0
(bring to the form: -3 (x + y) 2 + (y -1) 2 \u003d 0)
Answer: (-1; 1)
3. x2 + 3y2 + 2xy + 28y +98 = 0
(bring to the form: (x + y) 2 + 2 (y + 7) 2 \u003d 0)
Answer: (7; -7)
Conclusion.
In this scientific work, equations with two variables of the second degree were studied, methods for solving them were considered. The task is completed, a shorter solution method is formulated and described, based on selecting a full square and replacing the equation with an equivalent system of equations, as a result, the procedure for finding the roots of an equation with two variables is simplified.
An important point of the work is that the method under consideration is used in solving various mathematical problems associated with a quadratic function, constructing second-order curves, and finding the largest (smallest) value of expressions.
Thus, the technique of expanding a second-order equation with two variables into a sum of squares has the most numerous applications in mathematics.
§ 1 Selection of the roots of the equation in real situations
Consider this real situation:
Master and apprentice together made 400 pieces to order. Moreover, the master worked for 3 days, and the student for 2 days. How many pieces did each one make?
Let us compose an algebraic model of this situation. Let the master make parts in 1 day. And the student is at the details. Then the master will make 3 parts in 3 days, and the student will make 2 parts in 2 days. Together they will make 3x + 2 parts. Since, according to the condition, 400 parts were manufactured in total, we get the equation:
The resulting equation is called a linear equation with two variables. Here we need to find a pair of numbers x and y, under which the equation will take the form of a true numerical equality. Note that if x \u003d 90, y \u003d 65, then we get the equality:
3 ∙ 90 + 65 ∙ 2 = 400
Since the correct numerical equality has been obtained, the pair of numbers 90 and 65 will be the solution to this equation. But the found solution is not unique. If x \u003d 96 and y \u003d 56, then we get the equality:
96 ∙ 3 + 56 ∙ 2 = 400
This is also a true numerical equality, which means that the pair of numbers 96 and 56 is also a solution to this equation. But a pair of numbers x = 73 and y = 23 will not be a solution to this equation. Indeed, 3 ∙ 73 + 2 ∙ 23 = 400 will give us an incorrect numerical equality 265 = 400. It should be noted that if we consider the equation in relation to this real situation, then there will be pairs of numbers that, being a solution to this equation, will not be a solution to a problem. For example, a couple of numbers:
x=200 and y=-100
is a solution to the equation, but the student cannot make -100 parts, and therefore such a pair of numbers cannot be the answer to the question of the problem. Thus, in each specific real situation, it is necessary to reasonably approach the selection of the roots of the equation.
Let's sum up the first results:
An equation of the form ax + by + c \u003d 0, where a, b, c are any numbers, is called a linear equation with two variables.
The solution of a linear equation with two variables is a pair of numbers corresponding to x and y, for which the equation becomes a true numerical equality.
§ 2 Graph of a linear equation
The very notation of the pair (x; y) prompts us to think about the possibility of depicting it as a point with coordinates xi y on the plane. So, we can get a geometric model of a particular situation. For example, consider the equation:
2x + y - 4 = 0
We select several pairs of numbers that will be solutions to this equation and construct points with the found coordinates. Let these be points:
A(0; 4), B(2; 0), C(1; 2), D(-2; 8), E(- 1; 6).
Note that all points lie on the same line. Such a straight line is called the graph of a linear equation with two variables. It is a graphical (or geometric) model of a given equation.
If a pair of numbers (x; y) is a solution to the equation
ax + y + c = 0, then the point M(x; y) belongs to the graph of the equation. It can also be said vice versa: if the point M(x; y) belongs to the graph of the equation ax + wu + c = 0, then the pair of numbers (x; y) is the solution to this equation.
From the geometry course we know:
To plot a straight line, 2 points are needed, therefore, to plot a linear equation with two variables, it is enough to know only 2 pairs of solutions. But guessing the roots of the procedure is not always convenient, not rational. You can act according to another rule. Since the abscissa of the point (variable x) is an independent variable, you can give it any convenient value. Substituting this number into the equation, we find the value of the variable y.
For example, let's say the equation is:

Let x \u003d 0, then we get 0 - y + 1 \u003d 0 or y \u003d 1. So, if x \u003d 0, then y \u003d 1. A pair of numbers (0; 1) is the solution to this equation. Let's set another value x = 2 for the variable x. Then we get 2 - y + 1 = 0 or y = 3. A pair of numbers (2; 3) is also a solution to this equation. According to the two points found, it is already possible to plot the equation x - y + 1 \u003d 0.
You can also do this: first give some specific value to the variable y, and only then calculate the value of x.
§ 3 System of equations
Find two natural numbers whose sum is 11 and whose difference is 1.
To solve this problem, we first compose a mathematical model (namely, an algebraic one). Let the first number be x and the second be y. Then the sum of the numbers x + y \u003d 11 and the difference of the numbers x - y \u003d 1. Since both equations deal with the same numbers, these conditions must be met simultaneously. Usually in such cases a special notation is used. Equations are written one below the other and combined with curly brackets.

Such a record is called a system of equations.

Let us now construct sets of solutions for each equation, i.e. graphs of each of the equations. Let's take the first equation:
If x = 4, then y = 7. If x = 9, then y = 2.
Let's draw a straight line through the points (4;7) and (9;2).
Let's take the second equation x - y \u003d 1. If x \u003d 5, then y \u003d 4. If x \u003d 7, then y \u003d 6. Through the points (5; 4) and (7; 6) we will also draw a straight line. Obtained a geometric model of the problem. The pair of numbers (x; y) we are interested in must be a solution to both equations. In the figure, we see the only point that lies on both lines, this is the point of intersection of the lines.
Its coordinates are (6;5). Therefore, the solution to the problem will be: the first desired number is 6, the second is 5.
List of used literature:
- Mordkovich A.G., Algebra grade 7 in 2 parts, Part 1, Textbook for educational institutions / A.G. Mordkovich. - 10th ed., revised - Moscow, "Mnemosyne", 2007
- Mordkovich A.G., Algebra grade 7 in 2 parts, Part 2, Task book for educational institutions / [A.G. Mordkovich and others]; edited by A.G. Mordkovich - 10th edition, revised - Moscow, "Mnemosyne", 2007
- HER. Tulchinskaya, Algebra Grade 7. Blitz survey: a guide for students of educational institutions, 4th edition, revised and supplemented, Moscow, "Mnemozina", 2008
- Alexandrova L.A., Algebra Grade 7. Thematic test papers in a new form for students of educational institutions, edited by A.G. Mordkovich, Moscow, "Mnemosyne", 2011
- Aleksandrova L.A. Algebra 7th grade. Independent work for students of educational institutions, edited by A.G. Mordkovich - 6th edition, stereotypical, Moscow, "Mnemosyne", 2010
In the 7th grade mathematics course, they first meet with equations with two variables, but they are studied only in the context of systems of equations with two unknowns. That is why a number of problems fall out of sight, in which certain conditions are introduced on the coefficients of the equation that limit them. In addition, methods for solving problems like “Solve an equation in natural or integer numbers” are also ignored, although problems of this kind are encountered more and more often in the materials of the Unified State Examination and at entrance exams.
Which equation will be called an equation with two variables?
So, for example, the equations 5x + 2y = 10, x 2 + y 2 = 20, or xy = 12 are two-variable equations.
Consider the equation 2x - y = 1. It turns into a true equality at x = 2 and y = 3, so this pair of variable values is a solution to the equation under consideration.
Thus, the solution of any equation with two variables is the set of ordered pairs (x; y), the values of the variables that this equation turns into a true numerical equality.
An equation with two unknowns can:
a) have one solution. For example, the equation x 2 + 5y 2 = 0 has a unique solution (0; 0);
b) have multiple solutions. For example, (5 -|x|) 2 + (|y| – 2) 2 = 0 has 4 solutions: (5; 2), (-5; 2), (5; -2), (-5; - 2);
in) have no solutions. For example, the equation x 2 + y 2 + 1 = 0 has no solutions;
G) have infinitely many solutions. For example, x + y = 3. The solutions to this equation will be numbers whose sum is 3. The set of solutions to this equation can be written as (k; 3 - k), where k is any real number.
The main methods for solving equations with two variables are methods based on the decomposition of expressions into factors, the selection of a full square, the use of the properties of a quadratic equation, the boundedness of expressions, and evaluation methods. The equation, as a rule, is transformed into a form from which a system for finding unknowns can be obtained.
Factorization
Example 1
Solve the equation: xy - 2 = 2x - y.
Decision.
We group the terms for the purpose of factoring:
(xy + y) - (2x + 2) = 0. Take out the common factor from each bracket:
y(x + 1) – 2(x + 1) = 0;
(x + 1)(y - 2) = 0. We have:
y = 2, x is any real number or x = -1, y is any real number.
Thus, the answer is all pairs of the form (x; 2), x € R and (-1; y), y € R.
Equality to zero of non-negative numbers
Example 2
Solve the equation: 9x 2 + 4y 2 + 13 = 12(x + y).
Decision.
Grouping:
(9x 2 - 12x + 4) + (4y 2 - 12y + 9) = 0. Now each parenthesis can be collapsed using the square difference formula.
(3x - 2) 2 + (2y - 3) 2 = 0.
The sum of two non-negative expressions is zero only if 3x - 2 = 0 and 2y - 3 = 0.
So x = 2/3 and y = 3/2.
Answer: (2/3; 3/2).
Evaluation method
Example 3
Solve the equation: (x 2 + 2x + 2) (y 2 - 4y + 6) = 2.
Decision.
In each bracket, select the full square:
((x + 1) 2 + 1)((y – 2) 2 + 2) = 2. Estimate  the meaning of the expressions in brackets.
the meaning of the expressions in brackets.
(x + 1) 2 + 1 ≥ 1 and (y - 2) 2 + 2 ≥ 2, then the left side of the equation is always at least 2. Equality is possible if:
(x + 1) 2 + 1 = 1 and (y - 2) 2 + 2 = 2, so x = -1, y = 2.
Answer: (-1; 2).
Let's get acquainted with another method for solving equations with two variables of the second degree. This method is that the equation is considered as square with respect to some variable.
Example 4
Solve the equation: x 2 - 6x + y - 4√y + 13 = 0.
Decision.
Let's solve the equation as a quadratic one with respect to x. Let's find the discriminant:
D = 36 - 4(y - 4√y + 13) = -4y + 16√y - 16 = -4(√y - 2) 2 . The equation will have a solution only when D = 0, i.e., if y = 4. We substitute the value of y into the original equation and find that x = 3.
Answer: (3; 4).
Often in equations with two unknowns indicate restrictions on variables.
Example 5
Solve the equation in integers: x 2 + 5y 2 = 20x + 2.
Decision.
Let's rewrite the equation in the form x 2 = -5y 2 + 20x + 2. The right side of the resulting equation, when divided by 5, gives a remainder of 2. Therefore, x 2 is not divisible by 5. But the square of a number that is not divisible by 5 gives a remainder of 1 or 4. Thus equality is impossible and there are no solutions.
Answer: no roots.
Example 6
Solve the equation: (x 2 - 4|x| + 5) (y 2 + 6y + 12) = 3.
Decision.
Let's select the full squares in each bracket:
((|x| – 2) 2 + 1)((y + 3) 2 + 3) = 3. The left side of the equation is always greater than or equal to 3. Equality is possible if |x| – 2 = 0 and y + 3 = 0. Thus, x = ± 2, y = -3.
Answer: (2; -3) and (-2; -3).
Example 7
For each pair of negative integers (x; y) satisfying the equation
x 2 - 2xy + 2y 2 + 4y = 33, calculate the sum (x + y). Answer the smallest amount.
Decision.
Select full squares:
(x 2 - 2xy + y 2) + (y 2 + 4y + 4) = 37;
(x - y) 2 + (y + 2) 2 = 37. Since x and y are integers, their squares are also integers. The sum of the squares of two integers, equal to 37, we get if we add 1 + 36. Therefore:
(x - y) 2 = 36 and (y + 2) 2 = 1 
(x - y) 2 = 1 and (y + 2) 2 = 36.
Solving these systems and taking into account that x and y are negative, we find solutions: (-7; -1), (-9; -3), (-7; -8), (-9; -8).
Answer: -17.
Do not despair if you have difficulties when solving equations with two unknowns. With a little practice, you will be able to master any equation.
Do you have any questions? Don't know how to solve equations with two variables?
To get help from a tutor -.
The first lesson is free!
blog.site, with full or partial copying of the material, a link to the source is required.
Nonlinear equations in two unknowns
Definition 1 . Let A be some set of pairs of numbers (x; y) . It is said that the set A is given numeric function z from two variables x and y , if a rule is specified, with the help of which a certain number is assigned to each pair of numbers from the set A.
Specifying a numerical function z of two variables x and y is often designate So:
where f (x , y) - any function other than the function
f (x , y) = ax+by+c ,
where a, b, c are given numbers.
Definition 3 . Equation (2) solution name a pair of numbers x; y) , for which formula (2) is a true equality.
Example 1 . solve the equation
Since the square of any number is non-negative, it follows from formula (4) that the unknowns x and y satisfy the system of equations

the solution of which is a pair of numbers (6 ; 3) .
Answer: (6; 3)
Example 2 . solve the equation
Therefore, the solution to equation (6) is an infinite number of pairs of numbers kind
(1 + y ; y) ,
where y is any number.
linear
Definition 4 . Solving the system of equations

name a pair of numbers x; y) , substituting them into each of the equations of this system, we obtain the correct equality.
Systems of two equations, one of which linear, have the form
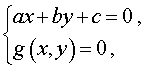
g(x , y)
Example 4 . Solve a system of equations
Decision . Let us express the unknown y from the first equation of system (7) in terms of the unknown x and substitute the resulting expression into the second equation of the system:


Solving the Equation
x 1 = - 1 , x 2 = 9 .
Hence,
y 1 = 8 - x 1 = 9 ,
y 2 = 8 - x 2 = - 1 .


Systems of two equations, one of which is homogeneous
Systems of two equations, one of which homogeneous, have the form

where a , b , c are given numbers, and g(x , y) is a function of two variables x and y .
Example 6 . Solve a system of equations
Decision . We will decide homogeneous equation
3x 2 + 2xy - y 2 = 0 ,
3x 2 + 17xy + 10y 2 = 0 ,
treating it like quadratic equation relative to unknown x :
 .
.
In case when x = - 5y, from the second equation of system (11) we obtain the equation
5y 2 = - 20 ,
which has no roots.
In case when
from the second equation of system (11) we obtain the equation
 ,
,
whose roots are numbers y 1 = 3 , y 2 = - 3 . Finding for each of these values y the corresponding value x , we obtain two solutions to the system: (- 2 ; 3) , (2 ; - 3) .
Answer: (- 2 ; 3) , (2 ; - 3)
Examples of solving systems of equations of other types
Example 8 . Solve the system of equations (MIPT)
Decision . We introduce new unknowns u and v , which are expressed in terms of x and y by the formulas:
To rewrite system (12) in terms of new unknowns, we first express the unknowns x and y in terms of u and v . It follows from system (13) that
We will decide linear system(14), eliminating the variable x from the second equation of this system. To this end, we perform the following transformations on system (14):
- we leave the first equation of the system unchanged;
- subtract the first equation from the second equation and replace the second equation of the system with the resulting difference.
As a result, system (14) is transformed into equivalent her system

from which we find
Using formulas (13) and (15), we rewrite the original system (12) as
System (16) has the first equation - linear, so we can express the unknown u from it in terms of the unknown v and substitute this expression into the second equation of the system.
